Multi-user Detection
| Introduction |
| Single User Detection (SUD) |
| Multi User Detection (MUD) |
| Simulation Result |
Introduction



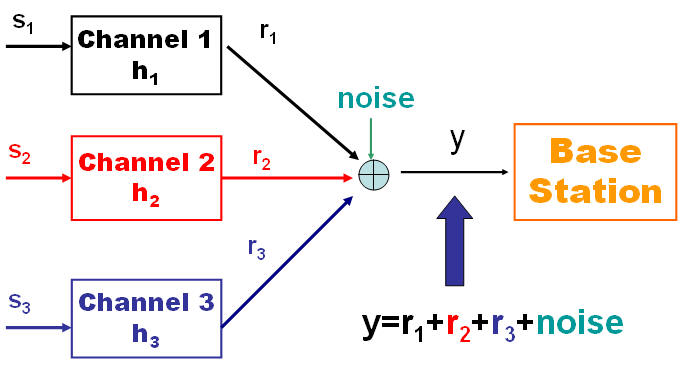

Single User Detection
Detection
•Single User Detection (SUD)
–Equal Gain Combining (EGC)
–Maximum Ratio Combining (MRC)
–Orthogonal Restoring Combing (ORC)
–Minimum Mean Square Error Combining (MMSE)
•Multi User Detection (MUD)
SUD
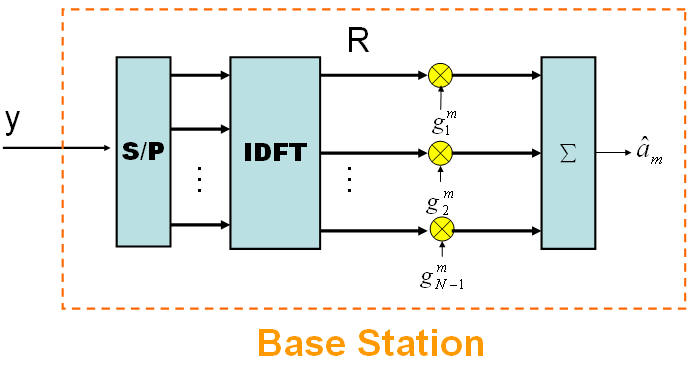
![]()
![]()
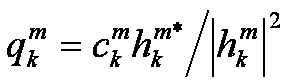

MAI
MUD
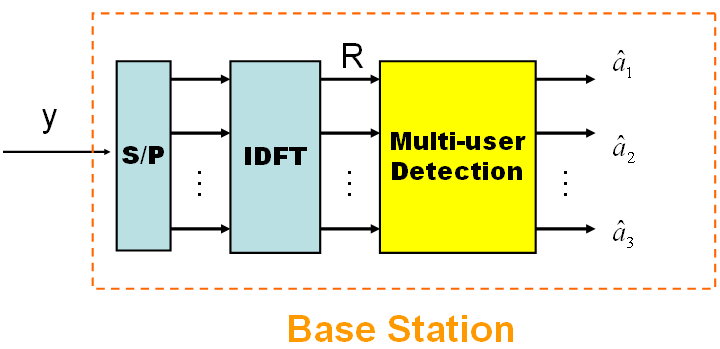
The Successive Interference Cancellation (SIC) detector takes a serial approach to interference cancellation. Each stage of this detector decisions, regenrates and cancels out one direct sequence user from the received signal, so that the remaining users see less MAI in the next stage. The result is that the strongest user will not benefit from any MAI reduction; the weakest user will however see a huge reduction in its MAI.
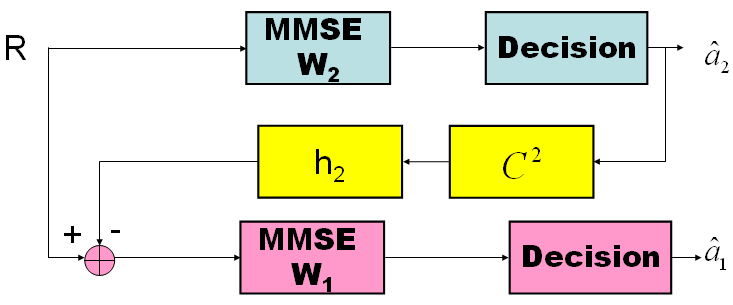
Parallel
Interference
Cancellation
(PIC)

